LIMITES DE FONCTIONS, CONTINUITÉ, DÉRIVATION, FONCTION LN

Logarithmes népériens

• Partie A

  On considère la fonction $f$ définie sur $]-1;+\infty[$ par :

  $f(x)=ax+b+3\ln(x+1)$ où $a$ et $b$ désignent 2 réels que l'on déterminera dans la question 2.
  La figure ci-dessous représente une partie de cette courbe donnée par une calculatrice graphique.

  (Les graduations sont à l'unité.)

  

   

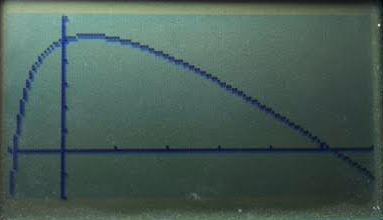
  La courbe $C$ représentant $f$ vérifie les conditions suivantes :

  Elle passe par le point $A(0 ;5)$ et elle admet une tangente horizontale au point $B$ d'abscisse $ \dfrac{1}{2}$.

  
  1) En utilisant les données de l'énonce, que peut-on dire du sens de variation de $f$ ?

  2) Déterminer les réels $a$ et $b$.
  
  

  Partie B

  On suppose désormais que la fonction $f$ est définie sur $]-1;+\infty[$ par : 
  $f(x)=-2x+5+3\ln(x+1)$.

  1) a) Calculer la limite de $f$ en $-1$. Interpréter graphiquement le résultat.

  b) Calculer la limite de $f$ au voisinage de $+\infty$.

  2) Calculer $f'(x)$ et étudier les variations de $f$. Dresser le tableau de variation de $f$.
  Préciser la valeur exacte du maximum de $f$.

  3) Tracer $C$ et les asymptotes éventuelles dans un plan muni d'un repère orthonormal $(O,I;J)$.
  Unités graphiques : 2cm.

  4) a) Montrer qu'il existe 2 réels $\alpha$ et $\beta$ tels que : $\alpha<0<\beta$ et $f(\alpha)=f(\beta)=0$.

  b) Donner une valeur approchée à $10^{-2}$ près par défaut de $\alpha$ et de $\beta$.

  c) En déduire le signe de $f(x)$ sur $]-1 ; +\infty[$.

  Afficher la correction

  ---