LIMITES DE FONCTIONS, CONTINUITÉ, DÉRIVATION, FONCTION LN

Annales

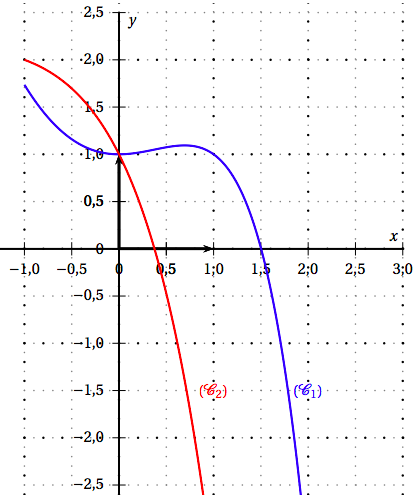
• La courbe $(C_1)$ ci-dessous représente, dans un repère orthonormé, une fonction $f$ définie et deux fois dérivable sur $[−1 ; 2]$.

  On note $f ′$ la fonction dérivée de $f$ et $f ′′$ la fonction dérivée seconde de $f$ . La courbe ($C_2$) ci-dessous représente, dans le repère orthonormé, la fonction $f ′′$ .

  Le point $A(0; 1)$ est situé sur la courbe ($C_1$). Le point $B$ est le point d’intersection de ($C_2$) avec l’axe des abscisses. Une valeur approchée de l’abscisse de $B$ est $0,37$. La tangente à la courbe ($C_1$) au point $A$ est horizontale.

  

  1. Par lecture graphique,

    a. Donner la valeur de $f (0)$.

    b. Donner la valeur de $f ′ (0)$.

    c. Étudier la convexité de $f$ sur $[−1 ; 2]$. Justifier la réponse.

  2. On admet désormais que la fonction $f$ est définie pour tout réel $x$ dans $[−1 ; 2]$ par : $f (x) = (1− x)e^x + x^2$ .

  Un logiciel de calcul formel donne les résultats suivants : 

  

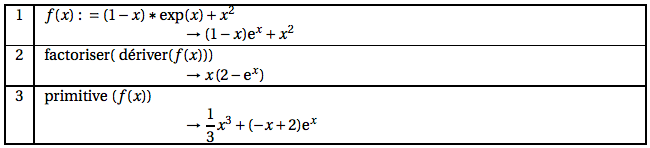
    a. Vérifier le résultat trouvé par le logiciel pour le calcul de $f ′ (x)$.

    b. Étudier le signe de $f ′ (x)$ puis dresser le tableau de variation de la fonction $f$ sur $[−1 ; 2]$.

  3. a. Justifier que l’équation $f (x) = 0$ possède une unique solution $\alpha$ dans $[−1 ; 2]$.

     b. Déterminer un encadrement de $\alpha$ d’amplitude $0,01$.

  4. Déterminer une équation de la tangente à ($C_1$) au point d’abscisse 1.

  5. a. Justifier la ligne 3 du tableau de calcul formel.

     b. On admet que la fonction $f$ est positive sur $[−1 ; 1]$. En déduire l’aire exacte, en unités d’aire, du domaine compris entre la courbe ($C_1$), l’axe des abscisses et les droites d’équation $x = −1$ et $x = 1$, puis en donner une valeur arrondie au dixième.

  Afficher la correction

  ---