LIMITES DE FONCTIONS, CONTINUITÉ, DÉRIVATION, FONCTION LN

Logarithmes népériens

• Partie A : étude d’une fonction

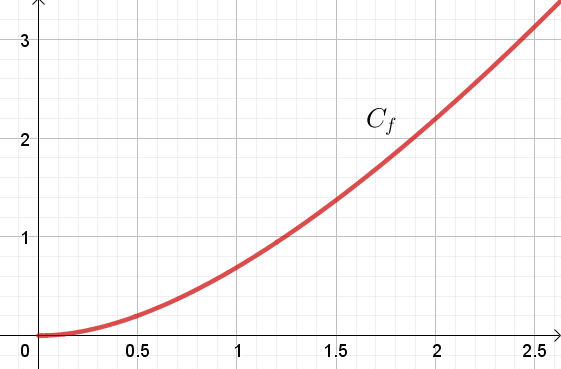
  Soit $f$ la fonction définie sur l'intervalle $[0;+\infty[$  par $f(x)= x\ln (x+1)$

  Sa courbe représentative (C) dans un repère orthogonal est donnée ci-dessous.

  

   

  1.a. Montrer que la fonction $f$ est strictement croissante sur l’intervalle $[0;+\infty[$.

  b. L’axe des abscisses est-il tangent à la courbe (C) au point O ?

  2. On pose $I =\displaystyle\int_0^1 \dfrac{x^2}{x+1}dx$ 

  a. Déterminer 3 réels $a$, $b$ et $c$ tels que pour tout $x\neq -1,\dfrac{x^2}{x+1}=ax+b+\dfrac{c}{x+1}$

  b. Calculer $I$

  3. Montrer que l'équation $f(x)=0,25$ admet une seule solution sur l'intervalle $[0;1]$. On note $\alpha$ cette solution. Donner un encadrement de $\alpha$ d'amplitude $10^{-2}$.

   

  Partie B : étude d’une suite

  La suite $(U)$ est définie pour tout entier $n$ par : $U_n =\displaystyle\int_0^1 x^n\ln(x+1)dx$  

  1. Déterminer le sens de variation de la suite $(U)$.

  La suite $(U)$ converge-t-elle?

  2. Démontrer que pour tout entier naturel $n$ non nul, $0\leq n\leq \dfrac{\ln(2)}{n+1}$ .

  En déduire la limite de la suite $(U)$.

  Afficher la correction

  ---