LIMITES DE FONCTIONS, CONTINUITÉ, DÉRIVATION, FONCTION LN

Annales

• Énoncé

  Le but de cet exercice est d’étudier la fonction $f$ définie sur l’intervalle $]0; +\infty[$ par :

  $f(x) = x \ ln \ (x^2) - \dfrac{1}{x}$

   

  Partie A : lectures graphiques

  On a tracé ci-dessous la courbe représentative $(C_f)$ de la fonction $f,$ ainsi que la droite $(T)$, tangente à la courbe $(C_f)$ au point $A$ de coordonnées $(1; −1).$ Cette tangente passe également par le point $B(0; −4).$

  

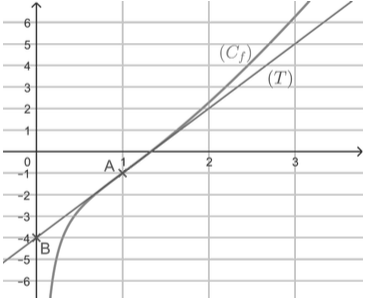
  1. Lire graphiquement $f'(1)$ et donner l’équation réduite de la tangente $(T).$

  2. Donner les intervalles sur lesquels la fonction $f$ semble convexe ou concave. Que semble représenter le point $A$ pour la courbe $(C_f)$ ? 

   

  Partie B : étude analytique

  1. Déterminer, en justifiant, la limite de $f$ en $+\infty,$ puis sa limite en 0.

  2. On admet que la fonction $f$ est deux fois dérivable sur l’intervalle $]0 ; +\infty[ .$

  a. Déterminer $f'(x)$ pour $x$ appartenant à l’intervalle $]0 ; +\infty[ . $

  b. Montrer que pour tout $x$ appartenant à l’intervalle $]0 ; +\infty[ ,$

  $f''(x)= \dfrac{2(x+1)(x-1)}{x^3}$

  3. a. Étudier la convexité de la fonction $f$ sur l’intervalle $]0 ; +\infty[ .$

  b. Étudier les variations de la fonction $f',$ puis le signe de $f'(x)$ pour $x$ appartenant à l’intervalle $]0 ; +\infty[.$

  En déduire le sens de variation de la fonction $f$ sur l’intervalle $]0 ; +\infty[.$

  4. a. Montrer que l’équation $f(x)=0$ admet une unique solution $\alpha$ sur l’intervalle $]0; +\infty[.$

  b. Donner la valeur arrondie au centième de $\alpha$ et montrer que $\alpha$ vérifie :

  $\alpha^2 = exp (\dfrac{1}{\alpha^2})$

  Afficher la correction

  ---