LIMITES DE FONCTIONS, CONTINUITÉ, DÉRIVATION, FONCTION LN

Annales

• Énoncé

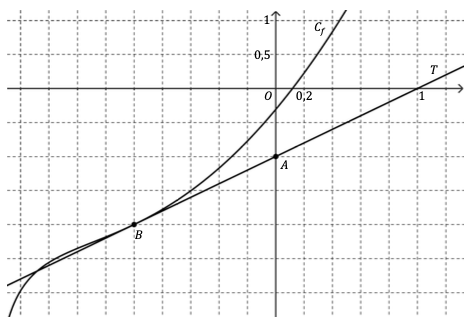
  On considère une fonction $f$ définie et deux fois dérivable sur $]−2;+\infty[.$ On note $C_f$ sa courbe représentative dans un repère orthogonal du plan, $f'$sa dérivée et $f''$ sa dérivée seconde. On a tracé ci-dessous la courbe $C_f$ et sa tangente $T$ au point $B$ d’abscisse −1.

  On précise que la droite $T$ passe par le point $A(0 ; −1).$

  

   

  Partie A : exploitation du graphique

  À l’aide du graphique, répondre aux questions ci-dessous.

  1. Préciser $f(−1)$ et $f'(−1).$

  2. La courbe $C_f$ est-elle convexe sur son ensemble de définition ? Justifier. 

  3. Conjecturer le nombre de solutions de l’équation $f(x) = 0$ et donner une valeur arrondie à 10⁻¹ près d’une solution.

   

  Partie B : étude de la fonction $f$

  On considère que la fonction $f$ est définie sur $]−2 ; +\infty[$ par $f(x) = x^2 + 2x − 1 + \ ln(x + 2),$ où $ln$ désigne la fonction logarithme népérien.

  1. Déterminer par le calcul la limite de la fonction $f$ en −2. Interpréter graphiquement ce résultat.

  On admet que $\displaystyle\lim_{x\to+\infty} f(x) = +\infty$

  2. Montrer que pour tout $x > −2, f'(x) = \dfrac{2x^2+6x+5}{x+2}$

  3. Étudier les variations de la fonction $f$ sur $]−2 ; +\infty[$ puis dresser son tableau de variations complet.

  4. Montrer que l’équation $f(x) = 0$ admet une unique solution $\alpha$ sur $]−2 ; +\infty[$ et donner une valeur arrondie de $\alpha$ à 10⁻² près.

  5. En déduire le signe de $f(x)$ sur $]−2;+\infty[.$

  6. Montrer que $C_f$ admet un unique point d’inflexion et déterminer son abscisse.

   

  Partie C : une distance minimale

  Soit $g$ la fonction définie sur $]−2 ; +\infty[$ par $g(x) = ln(x + 2).$

  On note $C_g$ sa courbe représentative dans un repère orthonormé $(O; I, J),$ représentée ci-dessous.

  Soit $M$ un point de $C_g$ d’abscisse $x.$

  Le but de cette partie est de déterminer pour quelle valeur de $x$ la distance $JM$ est minimale.

  On considère la fonction $h$ définie sur $]−2;+\infty[$ par $h(x)=JM^2$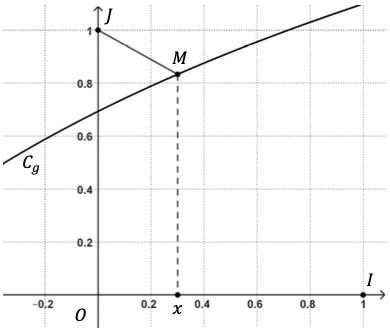

   

  

   

  1. Justifier que pour tout $x > −2,$ on a : $h(x) = x^2 + [ln(x + 2) − 1]^2.$

  2. On admet que la fonction $h$ est dérivable sur $]−2;+ \infty[$ et on note $h'$ sa fonction dérivée. On admet également que pour tout réel $x > −2,$

  $h'(x) = \dfrac{2f(x)}{x+2}$ où $f$ est la fonction étudiée en partie B.

  a. Dresser le tableau de variations de $h$ sur $]−2 ; +\infty[.$ Les limites ne sont pas demandées.

  b. En déduire que la valeur de $x$ pour laquelle la distance $JM$ est minimale est $\alpha$ où $\alpha$ est le nombre réel défini à la question 4 de la partie B.

  3. On notera $M_{\alpha}$ le point de $C_g$ d’abscisse $\alpha.$

  a. Montrer que $ ln(\alpha + 2) = 1 − 2 \alpha − \alpha^2.$

  b. En déduire que la tangente à $C_g$ au point $M_{\alpha}$ et la droite $(JM_{\alpha}$) sont perpendiculaires.

  On pourra utiliser le fait que, dans un repère orthonormé, deux droites sont perpendiculaires lorsque le produit de leurs coefficients directeurs est égal à −1.

  Afficher la correction

  ---