LIMITES DE FONCTIONS, CONTINUITÉ, DÉRIVATION, FONCTION LN

Primitives et calcul intégral

• Un nouveau modèle de mini-ordinateur portable est mis sur le marché. Soit $x$ la quantité d’appareils pouvant être vendus, exprimée en milliers.

  La fonction d’offre de cet appareil est la fonction $f$ définie sur l’intervalle $[0;35]$ par :

  $f(x) = 153 e^{0,05x}$

  Le nombre réel $f (x)$ désigne le prix unitaire en euros d’un appareil, proposé par les fournisseurs, en fonction de la quantité $x$, exprimée en milliers, d’appareils pouvant être vendus.

  La fonction de demande de cet appareil est la fonction $g$ définie sur l’intervalle $[0 ; 35]$ par :

  $g (x) = −116 \ln(x +1) + 504$

  Le nombre réel $g(x)$ désigne le prix unitaire en euros d’un appareil, accepté par les consommateurs, en fonction de la quantité $x$, exprimée en milliers, d’appareils disponibles.

  1) a) Démontrer que la fonction $f$ est strictement croissante sur l’intervalle $[0 ; 35]$.

  b) Démontrer que la fonction $g$ est strictement décroissante sur l’intervalle $[0 ; 35]$.

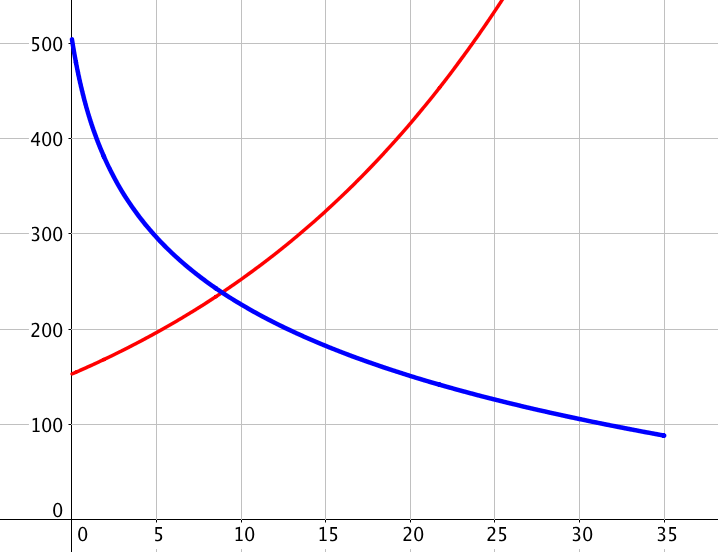
  c) Les courbes représentatives respectives $C_f$ et $C_g$ des fonctions $f$ et $g$, tracées dans un repère orthogonal, sont à imprimer (ou à reproduire) et à compléter.

  Lire avec la précision autorisée par le graphique une valeur approchée des coordonnées de leur point d’intersection $E$.

   

  2) Afin de déterminer les coordonnées du point $E$ de façon précise, on est amené à résoudre dans l’intervalle $[0 ; 35]$ l’équation $f (x) = g (x)$.

  Pour cela, on considère la fonction $h$ définie sur l’intervalle $[0 ; 35]$ par $h(x) = f (x) - g(x)$.

  a) Déterminer le sens de variation de la fonction $h$ sur l’intervalle $[0 ; 35]$.

  On pourra utiliser la question 1.

  b) Démontrer que l’équation $h(x) = 0$ admet une solution unique $x_0$ dans l’intervalle $[0 ; 35]$.

  c) À l’aide de la calculatrice, déterminer l’arrondi de $x_0$ au millième.

  d) On pose $y_0 = f (x_0)$. En utilisant la question précédente, calculer l’arrondi de $y_0$ au centième.

  e) Sachant que $y_0$ représente le prix unitaire d’équilibre de cet appareil, préciser ce prix à un centime d’euro près.

  Quel est le nombre d’appareils disponibles à ce prix ?

   

  3) On prendra dans cette question $x_0 = 8,871$ et $y_0 = 238,41$.

  a) Déterminer une primitive $F$ de la fonction $f$ sur l’intervalle $[0 ; 35]$.

  b) On appelle surplus des fournisseurs le nombre réel $S$ défini par la formule :

  $S = x_0 \times y_0 - \displaystyle\int^{x_0}_0 f(x) dx$ 

  Hachurer, sur le graphique de la feuille annexe à rendre avec la copie, le domaine du plan dont l’aire en unités d’aire est le nombre réel $S$.

  Déterminer la valeur arrondie au millième du nombre réel $S$.

    

  Afficher la correction

  ---