GÉOMÉTRIE, VECTEURS

Annales

• Énoncé

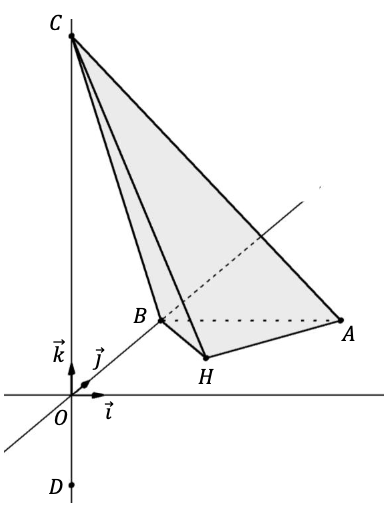
  L’espace est muni d’un repère orthonormé $(O ; \vec{i} ; \vec{j} ; \vec{k})$.

  On considère les points $A (5 ; 5 ; 0), B(0; 5; 0), C(0; 0; 10)$ et $D(0; 0; −\dfrac{5}{2} )$.

  

   

  Questions

  1. a. Montrer que $\vec{n_1}\begin{pmatrix}1 \\ -1 \\ 0 \end{pmatrix}$ est un vecteur normal au plan $(CAD)$.

  b. En déduire que le plan $(CAD)$ a pour équation cartésienne : $y - x = 0.$

  2. On considère que la droite $D$ de représentation paramétrique $\left \{ \begin{array}{lcc} x = \dfrac{5}{2}t \\ y = 5 - \dfrac{5}{2}t \\ z = 0 \end{array} \right.$ où $t \in \mathbb{R}.$

  a. On admet que la droite $D$ et le plan $(CAD)$ sont sécants en un point $H.$ Justifier que les coordonnées de $H$ sont $(\dfrac{5}{2} ; \dfrac{5}{2} ; 0).$

  b. Démontrer que le point $H$ est le projeté orthogonal de $B$ sur le plan $(CAD).$

  3. a. Démontrer que le triangle $ABH$ est rectangle en $H.$

  b. En déduire que l’aire du triangle $ABH$ est égale à $\dfrac{25}{4}.$

  4. a. Démontrer que $(CO)$ est la hauteur du tétraèdre $ABCH $ issue de $C.$

  b. En déduire le volume du tétraèdre $ABCH.$

  On rappelle que le volume d’un tétraèdre est donné par : $V = \dfrac{1}{3}Bh$ où $B$ est l’aire d’une base et $h$ la hauteur relative à cette base.

  5. On admet que le triangle $ABC$ est rectangle en $B.$ Déduire des questions précédentes la distance du point $H$ au plan $(ABC).$

  Afficher la correction

  ---