GRANDEURS COMPOSÉES ET UNITÉS

Annales

• Exercice 1

  Les longueurs sont en pixels. L’expression « s’orienter à 90 » signifie que l’on s’oriente vers la droite.

  On donne le programme suivant :

   

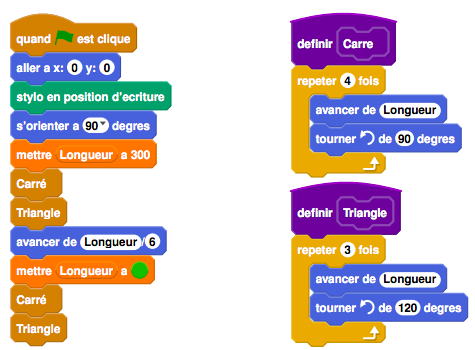
  1. On prend comme échelle 1 cm pour 50 pixels.

  a. Représenter sur votre copie la figure obtenue si le programme est exécuté jusqu’à la ligne 7 comprise.

  b. Quelles sont les coordonnées du stylo après l’exécution de la ligne 8 ?

  2. On exécute le programme complet et on obtient la figure ci-dessous qui possède un axe de symétrie vertical.

   

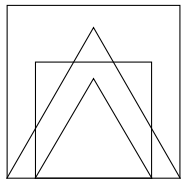
  Recopier et compléter la ligne 9 du programme pour obtenir cette figure.

  3. a. Parmi les transformations suivantes, translation, homothétie, rotation, symétrie axiale, quelle est la transformation géométrique qui permet d’obtenir le petit carré à partir du grand carré ? Préciser le rapport de réduction.

      b. Quel est le rapport des aires entre les deux carrés dessinés ?

   

  Exercice 2

  Le « hand-spinner » est une sorte de toupie plate qui tourne sur elle-même.

  

  On donne au « hand-spinner » une vitesse de rotation initiale au temps $t = $0, puis, au cours du temps, sa vitesse de rotation diminue jusqu’à l’arrêt complet du « hand-spinner ». Sa vitesse de rotation est alors égale à $0$. 

  Grâce à un appareil de mesure, on a relevé la vitesse de rotation exprimée en nombre de tours par seconde.

  Sur le graphique ci-dessous, on a représenté cette vitesse en fonction du temps exprimé en seconde :

  

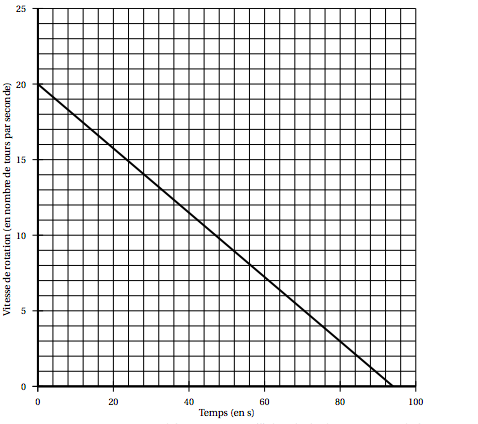
  1. Le temps et la vitesse de rotation du « hand-spinner » sont-ils proportionnels ? Justifier.

  2. Par lecture graphique, répondre aux questions suivantes :

     a. Quelle est la vitesse de rotation initiale du « hand-spinner » (en nombre de tours par seconde) ?

     b. Quelle est la vitesse de rotation du « hand-spinner » (en nombre de tours par seconde) au bout d’une minute et vingt secondes ?

     c. Au bout de combien de temps, le « hand-spinner » va-t-il s’arrêter ?

  3. Pour calculer la vitesse de rotation du « hand-spinner » en fonction du temps $t$, notée $V (t)$, on utilise la fonction suivante :

  $V (t) = −0,214× t +V_{\text{initiale}}$.

       • $t$ est le temps (exprimé en s) qui s’est écoulé depuis le début de rotation du « hand-spinner »;

       • $V_{\text{initiale}}$ est la vitesse de rotation à laquelle on a lancé le « hand-spinner » au départ.

     a. On lance le « hand-spinner » à une vitesse initiale de $20$ tours par seconde. Sa vitesse de rotation est donc donnée par la formule :

  $V (t) = −0,214× t +20$.

  Calculer sa vitesse de rotation au bout de $30$ s.

     b. Au bout de combien de temps le hand-spinner va-t-il s’arrêter ? Justifier par un calcul.

     c. Est-il vrai que, d’une manière générale, si l’on fait tourner le hand-spinner deux fois plus vite au départ, il tournera deux fois plus longtemps ? Justifier.

   

  Afficher la correction

  ---