GÉOMÉTRIE DANS L'ESPACE

Annales

• Pour obtenir l’octogone $EFGHIJKL$ ci-dessous, on retire quatre triangles rectangles isocèles identiques des coins d’un carré $ABCD$ de côté 5 m.

  

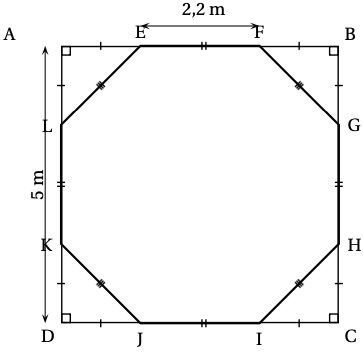
  On donne : 
  $AD$ = 5 m ;
  $EF$ = 2,2 m. 

  1. a. Montrer que la longueur $AE$ est égale à 1,4 m.

  1. b. Montrer que l’aire du triangle $AEL$ est égale à 0,98 m².

  1. c. En déduire que l’aire de l’octogone est égale à 21,08 m²

   

  Cet octogone a les mêmes dimensions que la surface d’une piscine de hauteur 1,50 m. On souhaite remplir cette piscine aux trois quarts de sa hauteur.

  2. a. Montrer que le volume d’eau nécessaire est environ égal à 24 m.

  2. b. Sachant que le débit du robinet utilisé pour remplir la piscine est de 12 L/min, calculer la durée de remplissage de ces 24 m³ d’eau.

  Donner le résultat en heures et minutes.

  Rappel : 1 m³ = 1 000 L.

  Afficher la correction

  ---