CALCUL INTÉGRAL

Annales

• Énoncé

  Partie A : étude de la fonction $f$

  La fonction $f$ est définie sur l'intervalle $]0; +\infty[$ par : $f(x) = x − 2 + 1 \ ln \ x,$ où $ln$ désigne la fonction logarithme népérien. On admet que la fonction $f$ est deux fois dérivable sur $]0; +\infty[$, on note $f'$ sa dérivée et $f''$ sa dérivée seconde.

   

  1. a. Déterminer, en justifiant, les limites de $f$ en $0$ et en $+\infty.$

  b. Montrer que pour tout $x$ appartenant à $]0; +\infty[$, on a : $f'(x) = \dfrac{2x+1}{2x}$.

  c. Étudier le sens de variation de $f$ sur $]0; +\infty[$.

  d. Étudier la convexité de $f$ sur $]0; +\infty[$.

  2. a. Montrer que l'équation $f(x) = 0$ admet dans $]0; +\infty[$ une solution unique qu'on notera $\alpha$ et justifier que $\alpha$ appartient à l’intervalle $[1 ; 2].$

  b. Déterminer le signe de $f(x)$ pour $x \in ]0; +\infty[$.

  c. Montrer que $ln(\alpha) = 2(2 − \alpha).$

   

  Partie B : étude de la fonction $g$

  La fonction $g$ est définie sur $]0;1]$ par $g(x) = -g(x)=−\dfrac{7}{8}x^2+x−\dfrac{1}{4}x^2 \ ln \ x.$

  On admet que la fonction $g$ est dérivable sur $]0 ; 1] $ et on note $g'$ sa fonction dérivée.

  1. Calculer $g'(x)$ pour $x \in ]0 ; 1]$ puis vérifier que $g'(x) = xf \dfrac{1}{x}.$

  2. a. Justifier que pour $x$ appartenant à l’intervalle $]0 ;\dfrac{1}{\alpha}[,$ on a $f \dfrac{1}{x} > 0.$

  b. On admet le tableau de signes suivant :

  

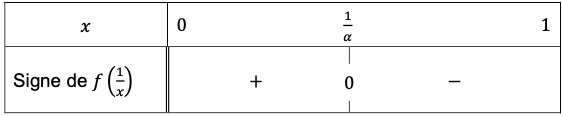
  En déduire le tableau de variations de $g$ sur l’intervalle $]0 ; 1].$ Les images et les limites ne sont pas demandées.

   

  Partie C : un calcul d’aire

  On a représenté sur le graphique ci-dessous :

  - La courbe $C$ de la fonction $g$ ;

  - La parabole $P$ d’équation $y=−\dfrac{7}{8}x^2+x$ sur l’intervalle $]0 ; 1].$

  

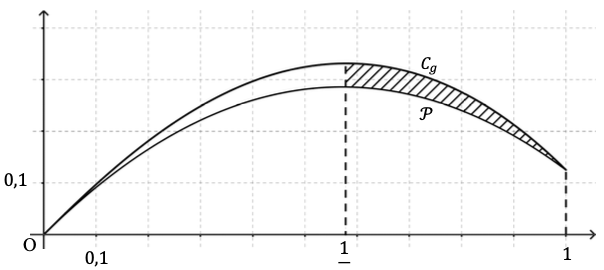
  On souhaite calculer l’aire $A$ du domaine hachuré compris entre les courbes $C_g$ et $P$ les droites d’équations $x = \dfrac{1}{\alpha}$ et $x = 1.$

  On rappelle que $ln(\alpha) = 2(2 - \alpha).$

   

  1. a. Justifier la position relative des courbes $C_g$ et $P$ sur l’intervalle $]0 ; 1].$

  b. Démontrer l’égalité :

  $\displaystyle \int_{\frac{1}{\alpha}}^1 x^2 \ ln \ x \ dx = \dfrac{-\alpha^3 - 6 \alpha + 13}{9 \alpha^3}$

  2. En déduire l’expression en fonction de $\alpha$ de l’aire $A.$

  Afficher la correction

  ---