CALCUL INTÉGRAL

Annales

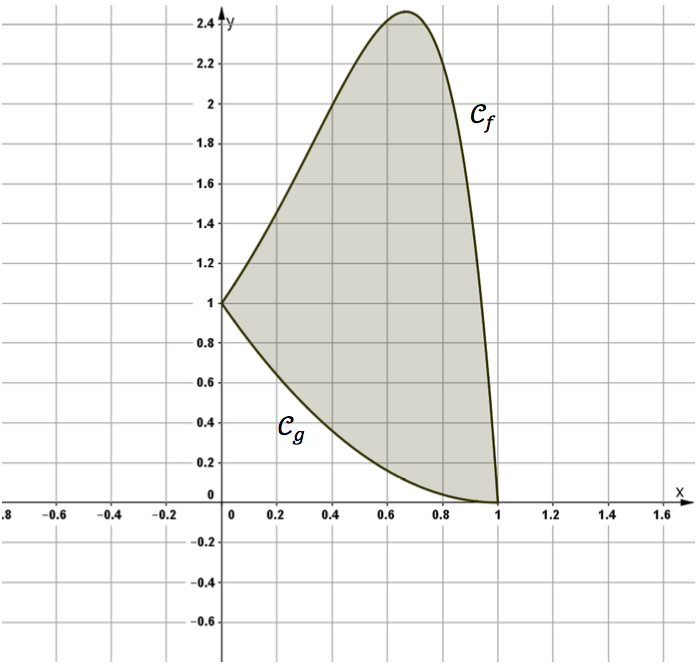
• Une entreprise souhaite utiliser un motif décoratif pour sa communication. Pour réaliser ce motif, on modélise sa forme à l'aide de deux fonctions $f $ et $g$ définies par :

  pour tout réel $x$ de $[0 ; 1], f(x) = (1 − x)e^{3x}$ et $g(x) = x^2 − 2x + 1.$

  Leurs courbes représentatives seront notées respectivement $Cf$ et $Cg.$

  

  PARTIE A

  Un logiciel de calcul formel donne les résultats suivants.

  dériver((1-x)*exp(3x))

                : -3x*exp(3*x)+2*exp(3*x)

  factoriser(-3x*exp(3*x)+2*exp(3*x))

                : exp(3x)*(-3x+2)

  factoriser(dériver(exp(3x)*(-3x+2)))

                : 3*exp(3*x)(1-3x)

   

  Lecture : la dérivée de la fonction $f$ est donnée par $f'(x) = −3xe^{3x} + 2e^{3x},$ ce qui, après factorisation, donne $f'(x) = (−3x + 2)e^{3x}.$

   

  1) Étudier sur $[0 ; 1]$ le signe de la fonction dérivée $f',$ puis donner le tableau de variation de $f$ sur $[0 ; 1]$ en précisant les valeurs utiles.

  2) La courbe $Cf$ possède un point d’inflexion. Déterminer ses coordonnées.

   

  PARTIE B

  On se propose de calculer l’aire de la partie grisée sur le graphique.

  1) Vérifier que les points $A$ et $B$ de coordonnées respectives $(1 ; 0)$ et $(0 ; 1)$ sont des points communs aux courbes $Cf$ et $Cg$.

   

  2) On admet que : pour tout $x$ dans $[0 ; 1], f(x) − g(x) = (1 – x)(e^{3x}– 1 + x).$

  a) Justifier que pour tout $x$ dans $[0 ; 1], e^{3x}– 1 \geq 0.$

  b) En déduire que pour tout $x$ dans $[0 ; 1], e^{3x}– 1 + x \geq 0.$

  c) Étudier le signe de $f(x) − g(x)$ pour tout $x$ dans $[0 ; 1].$

   

  3) a) Calculer $ \int_{0}^{1} g(x) dx $

   

  b) On admet que :

   

  $\int_{0}^{1} f(x) dx = \frac{e^3-4}{9}$

  Calculer l’aire $S,$ en unité d’aire, de la partie grisée. Arrondir le résultat au dixième.

  Afficher la correction

  ---