GÉOMÉTRIE, VECTEURS

Annales

• On considère le cube $ABCDEFGH$ de côté $1$, le milieu $I$ de $[EF]$ et $J$ le symétrique de $E$ par rapport à $F$. 

  

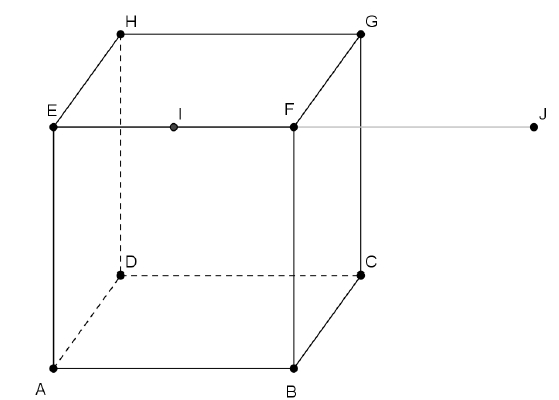
  Dans tout l'exercice, l'espace est rapporté au repère orthonormé $(A; \vec{AB};\vec{AD};\vec{AE})$

  1. a. Par lecture graphique, donner les coordonnées des points $I$ et $J$. 

  b. En déduire les coordonnées des vecteurs $\vec{DJ}$ ; $\vec{BI}$ et $\vec{BG}$

  c. Montrer que $\vec{DJ}$ est un vecteur normal au plan $(BGI)$. 

  d. Montrer qu’une équation cartésienne du plan $(BGI)$ est : $2x-y+z=0$

   

  2. On note $d$ la droite passant par $F$ et orthogonale au plan $(BGI)$. 

  a. Déterminer une représentation paramétrique de la droite $d$.

  b. On considère le point $L$ de coordonnées  $(23;16;56)$. 

  Montrer que $L$ est le point d’intersection de la droite $d$ et du plan $(BGI)$. 

   

  3. On rappelle que le volume $V$ d'une pyramide est donné par la formule 

  $V=\dfrac{1}{3}\times \mathcal{B} \times h$

  où $\mathcal{B}$ est l'aire d’une base et $h$ la hauteur associée à cette base. 

  a. Calculer le volume de la pyramide $FBGI$. 

  b. En déduire l'aire du triangle $BGI$.

  Afficher la correction

  ---