PROBABILITÉS

Annales

• Cet exercice est un questionnaire à choix multiples. Pour chaque question, une seule des quatre réponses proposées est correcte.

  Reporter sur la copie le numéro de la question ainsi que la lettre correspondant à la réponse choisie. Une réponse exacte rapporte 1 point. Une réponse fausse, une réponse multiple ou l’absence de réponse ne rapporte ni n’enlève aucun point. Aucune justification n’est demandée.

  Les parties A et B sont indépendantes.

   

  Partie A

  Dans un établissement scolaire, 30 % des élèves sont inscrits dans un club de sport, et parmi eux, 40 % sont des filles.

  Parmi ceux n’étant pas inscrits dans un club de sport, 50 % sont des garçons.

  Pour tout évènement $E$, on note $\overline E$ l’évènement contraire de $E$ et $p(\overline E)$ sa probabilité.

  Pour tout évènement $F$ de probabilité non nulle, on note $P_F(E)$ la probabilité de $E$ sachant que $F$ est réalisé.

  On interroge un élève au hasard et on considère les évènements suivants :

  • $S$ : « l’élève est inscrit dans un club de sport »

  • $F$ : « l’élève est une fille »

  La situation est représentée par l’arbre pondéré ci-contre.

  

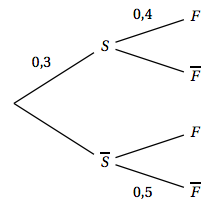
  1. La probabilité $p_F(S)$ est la probabilité que l’élève soit :

     a. inscrit dans un club de sport sachant que c’est un garçon;

     b. un garçon inscrit dans un club de sport;

     c. inscrit dans un club de sport ou un garçon;

     d. un garçon sachant qu’il est inscrit dans un club de sport.

  2. On admet que $P(F) = 0,47$. La valeur arrondie de $P_F (S)$ est :

        a. 0,141                b. 0,255             c. 0,400              d. 0,638

   

  Partie B

  Soit $g$ la fonction définie sur $[−1 ; 4]$ par $g (x) = −x^3 +3x^2 −1$ et $C_g$ sa courbe représentative dans un repère.

  1. La tangente à la courbe $C_g$ au point d’abscisse $1$ a pour équation :

        a. $y = −3x^2 +6x$            b. $y = 3x −2$            c. $y = 3x −3$             d. $y = 2x −1$

  2. La valeur moyenne de la fonction $g$ sur l’intervalle $[−1 ;a]$ est nulle pour :

        a. $a = 0$              b. $a = 1$                c. $a = 2$            d. $a = 3$

  Afficher la correction

  ---