L'ÉNERGIE : CONVERSIONS ET TRANSFERTS

L’énergie : conversions et transferts

• La volonté d'économiser l'énergie utilisée pour chauffer les bâtiments privés ou publics amène les particuliers, les entreprises ou les pouvoirs publics à opter pour des murs Trombe-Michel, du nom de ses deux inventeurs.

  Un mur Trombe-Michel est constitué essentiellement d'un double vitrage extérieur exposé aux rayonnements solaires, derrière lequel se trouve à environ une dizaine de centimètres un épais mur de béton qui s'intègre à la façade sud du bâtiment dont la surface extérieure est peinte en noir mat. En outre, de l'air circule entre le double vitrage et le mur peint en noir.

  Principe du mur Trombe-Michel

  

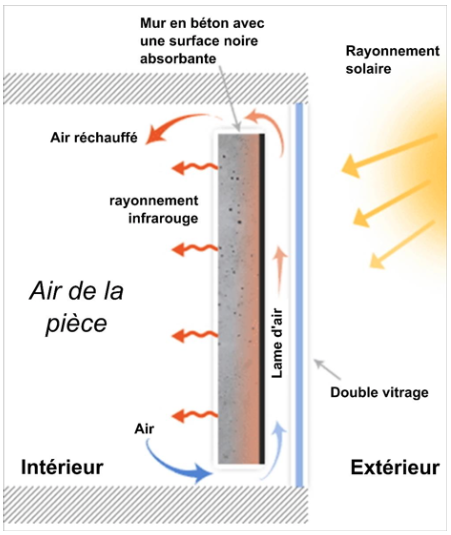
  Source : ecosources.info - Portail des énergies renouvelables et de l'écoconstruction

   

  Les professionnels du bâtiment mettent en avant trois avantages au mur Trombe-Michel : l'amélioration de l'isolation de la façade, le préchauffage de la lame d'air qui circule entre le mur en béton et le double vitrage, la restitution nocturne des apports énergétiques emmagasinés le jour.

  Données :

  

   

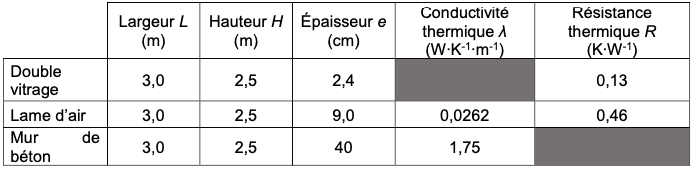
  A. Les trois modes de transfert thermique

  A.1. Citer les trois modes de transfert thermique.

  A.2. Citer, pour chacun de ces modes de transfert thermique, un exemple mis en oeuvre dans un mur Trombe-Michel.

   

  B. Isolation de la façade

  La résistance thermique notée $R$ d'une paroi s'exprime en $K.W^{-1}.$ Elle est modélisée par l'expression $R =\dfrac{e}{\lambda . S}$ avec $S$ la surface de la paroi, $e$ son épaisseur et ${\lambda}$ la conductivité thermique du matériau.

  La résistance thermique d'une paroi constituée de plusieurs couches successives de matériaux différents est la somme des résistances thermiques de chaque couche.

  Pour le mur Trombe-Michel, la résistance thermique de l'ensemble {mur + double vitrage} sans lame d'air est notée $R_1$ et la résistance de l'ensemble {mur + double vitrage + lame d'air} est notée $R_2.$

  On considère que la température extérieure est de 5,0 °C et que la température à l'intérieur de la pièce est de 19 °C.

  B.1.  Exprimer les flux thermiques ${\phi_1}$ et ${\phi_2}$ correspondant respectivement aux résistances $R_1$ et $R_2,$ puis calculer leurs valeurs.

  B.2.  En exploitant les valeurs obtenues, conclure quant à l'efficacité de la lame d'air.

   

  C. Chauffage de la pièce

  Le mur Trombe-Michel sert à chauffer une pièce qui contient 30 m³ d'air assimilé à un gaz parfait. Initialement la température de l'air a une valeur de 19,0 °C et atteint finalement la valeur de 23,0 °C.

  La variation d'énergie interne d'un gaz parfait, de capacité thermique $C,$ pour une variation de température $\Delta T$ est exprimée par la relation : $\Delta U = C.\Delta T.$ On donne la valeur de la capacité thermique de l'air contenu dans la pièce : $C = 39,2 \ kJ.K^{-1} .$

  C.1. Calculer la variation de l'énergie interne de l'air contenu dans la pièce.

   

  Le flux d'énergie solaire $F_{solaire}$ reçu par le double vitrage est estimé à 675 W. On estime à 25 % le pourcentage de l'énergie solaire transférée à l'air de la pièce.

  C.2. Déterminer la valeur de la durée nécessaire au réchauffement de l'air de la pièce de 19 °C à 23 °C.

   

  D. Flux thermique nocturne

  La nuit, le mur en béton restitue de la chaleur à l'air de la pièce en émettant un flux thermique total de l'ordre de 4 000 W.

  On considère que le mur en béton est à une température constante $T_m$ de 25 °C et l'air de la pièce à une température constante $T$ de 19 °C.

  Le flux thermique de convection ${\phi_c}$ s'exprime en fonction de la surface $S$ d'échange, de la différence de température $(T_m - T)$ et du coefficient de transfert thermique $h$ dont la valeur est $10 \ W.m^{-2}.K^{-1 }.$

  D.1. Choisir, en justifiant, parmi les trois expressions suivantes celle qui correspond à l'expression du flux thermique de convection :

  $\phi_c = \dfrac{h}{S}.(T_m - T)$    ;    $\phi_c = h.S.(T_m - T)$   ;   $\phi_c = \dfrac{h.S}{(T_m - T)}$

   

  D.2. En conduisant un raisonnement argumenté, déterminer si, la nuit, le mur restitue la chaleur à l'air de la pièce uniquement selon un mode convectif. Commenter.

  Afficher la correction

  ---