L'ÉNERGIE : CONVERSIONS ET TRANSFERTS

Comprendre : Énergie, matière et rayonnement

• Un centre de données (datacenter en anglais) est un lieu où se trouvent regroupés les équipements constituant le système d’information de l’entreprise (ordinateurs centraux, serveurs, baies de stockage, équipements réseaux et de télécommunications, etc.). Les plus connus sont ceux de Google, Facebook, Apple, etc.

  Au Val d’Europe, en Seine-et-Marne, le centre de données de Natixis permet de chauffer le nouveau centre aquatique et une pépinière d’entreprises. Piscine et pépinière d’entreprises (près de $6000 \ m^2$ au total) sont pourtant loin d’utiliser toute l’énergie disponible. Selon Dalkia, la filiale commune de Veolia et d’EDF qui exploite le réseau de chauffage, le centre de données peut chauffer jusqu’à $600 000 \ m^2$. Un centre de données de cette importance, avec de telles batteries de serveurs à alimenter et à refroidir en permanence, consomme une énergie électrique considérable : autant qu’une ville moyenne de $50 000$ habitants. $30 \%$ de cette énergie est utilisée pour le refroidissement des serveurs. Plutôt que de gaspiller en pure perte cette énergie, autant récupérer la chaleur que dégage la climatisation.

  D’après le site www.alliancy.fr

   

  Données numériques :

  Matériau	Laine de verre	Polystyrène	Laine de roche	béton armé	Polymère
  Conductivité thermique $\lambda \ (W.K^{-1}m^{-1})$	$0,032$	$0,038$	$0,034$	$2,2$	$0,18$

  $1 \ kWh = 3,6 \times 10^6 \ J$

   

  Données : 

  Conditions d’obtention du label HQE (Haute Qualité Environnementale) :
  On note $Z$ la résistance thermique d’une paroi ayant une surface de $1 \ m^2$. Pour obtenir le label HQE, la valeur de $Z$ doit avoir une valeur minimale notée $Z_{HQE}$. Cette valeur minimale dépend de la paroi étudiée. Les valeurs minimales sont données sur le schéma ci-dessous.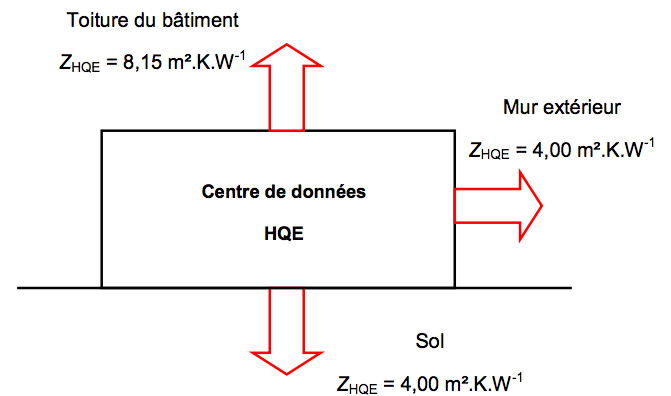

  

   

  L'énergie thermique transférée à un système par un flux thermique $\phi$ pendant la durée $\Delta t$ est : $Q = \phi \Delta t$ avec :
  $Q$ : énergie thermique transférée ($J$)
  $\phi$ : flux thermique ($W$)
  $\Delta t$ : durée du transfert ($s$)

  Lorsque les températures extérieure $T_{ext}$ et intérieure $T_{int}$ sont constantes au cours du temps, avec $T_{int} > T_{ext}$, le flux thermique $\phi$ à travers une paroi s'exprime par :

  $\phi = \dfrac{T_{int} - T_{ext}}{R_{th}}$

  avec :
  $\phi$ : flux thermique ($W$)
  $R_{th}$ : résistance thermique de la paroi considérée ($K.W^{-1}$)

  La résistance thermique $R_{th}$ dune paroi plane est définie par la relation : 

  $R_{th} = \dfrac{Z}{S}$ avec $Z = \dfrac{e}{\lambda}$

  avec :
  $e$ : épaisseur de la paroi ($m$)
  $\lambda$ : conductivité thermique (en unité du système international USI)
  $S$ : surface de la paroi ($m^2$)
  $Z$ : résistance thermique d’une paroi ayant une surface égale à $1 \ m^2$

  Les résistances thermiques de plusieurs matériaux superposés s’ajoutent.
  
  

   

  Partie 1 - Isolation thermique des murs du centre de données

  Lors de l’élaboration des plans du centre de données, l’objectif était d’obtenir le label HQE pour le bâtiment. Dans toute cette partie, on raisonnera sur un mur extérieur dont la surface est de $1,0 \ m^2$.

  1) Quelle devrait être l’épaisseur du mur extérieur si celui-ci n’était constitué que de béton armé ?

  

  L’épaisseur des murs en béton armé est en réalité de $20 \ cm$. Pour améliorer la résistance thermique des murs, on se propose d’ajouter une couche d’isolant et de la recouvrir de panneaux en polymère de $5,0 \ cm$ d’épaisseur afin de réaliser une étanchéité à l’eau et à l’air (schéma ci-dessus).

  2) L’isolant choisi est la laine de verre. Justifier ce choix.

  3) Déterminer l’épaisseur minimale de laine de verre nécessaire pour que la condition d’obtention du label HQE soit vérifiée.

   

  Partie 2 - Bilan thermique du centre de données

  Un bâtiment contenant $20 000$ serveurs a une longueur de $80  \ m$, une largeur de $50\ m$ et une hauteur de $10\ m$. Le reste du bâtiment contient des bureaux et des locaux techniques qui ne seront pas pris en compte.
  Le bâtiment respecte les normes HQE.
  La puissance électrique consommée par un serveur est de $480 \ W$.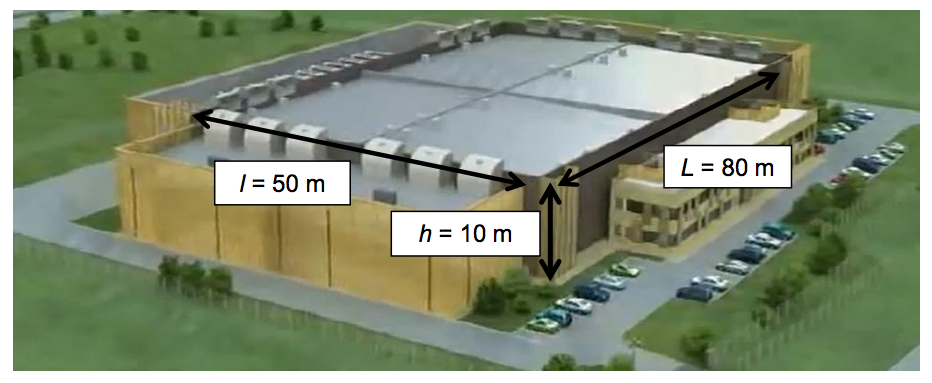

   

   

   

   

   

   

   

  D'après www.econovista.blogspot.f

  On admettra que toute l’énergie électrique consommée par les $20 000$ serveurs est transformée en énergie thermique.

  On se placera dans la situation où la valeur de la résistance thermique de chaque paroi de surface de $1,0\ m^2$ est égale à la valeur minimale $Z_{HQE}$.

   

  1) Citer les trois modes de transfert qui permettent aux ordinateurs de céder de l’énergie thermique à la pièce où ils sont stockés.

  2) Montrer, dans le cadre des hypothèses faites, que l’énergie thermique $Q_{serveurs}$ libérée en une journée par les serveurs est égale à $8,3 \times 10^{11} \ J$.

  3) Les températures moyennes au Val d’Europe au cours d’une journée d’hiver sont rassemblées dans le tableau ci-dessous.

  	Air extérieur	Sol	Intérieur
  Température ($°C$)	$7,0$	$11$	$23$

  A) Calculer le transfert thermique $Q_{sol}$ à travers le sol pour une journée d’hiver.

  B) Sachant que les transferts thermiques à travers les murs et la toiture, pour une journée d’hiver, sont respectivement $Q_{murs} = 9,0 \times 10^8 \ J$ et $Q_{toiture} = 6,8 \times 10^8 \ J$, déterminer l’énergie thermique totale perdue par l’ensemble des parois du centre de données au cours d’une journée d’hiver.

  4) Que risque-t-il de se passer au niveau du bâtiment du centre de données si rien n’est fait ?

   

   

  Partie 3 - Valorisation de l’énergie produite par les serveurs 

  1) L’énergie thermique libérée en six mois par les serveurs est égale à $1,5 \times 10^{14} \ J$.
  On estime qu’il faut $50 \ kWh$ pour chauffer $1 \ m^2$ de logement récent durant les six mois de l’année où le chauffage est en fonctionnement.
  Quelle surface de logement ce système permet-il de chauffer, durant ces six mois, grâce au centre de données ?
  La valeur annoncée dans le texte introductif est-elle réaliste ? 

  2) Plutôt que de rejeter de l’air chaud à l’extérieur, il est possible d’utiliser l’énergie thermique libérée pour chauffer des bureaux ou des logements voisins. Une machine thermique, aussi appelée climatiseur, refroidit l’air du centre de données et chauffe l’eau d’un circuit d’eau chaude primaire. Le circuit d’eau chaude primaire permet ensuite de chauffer l’eau des différents bâtiments par l’intermédiaire d’un échangeur.

  

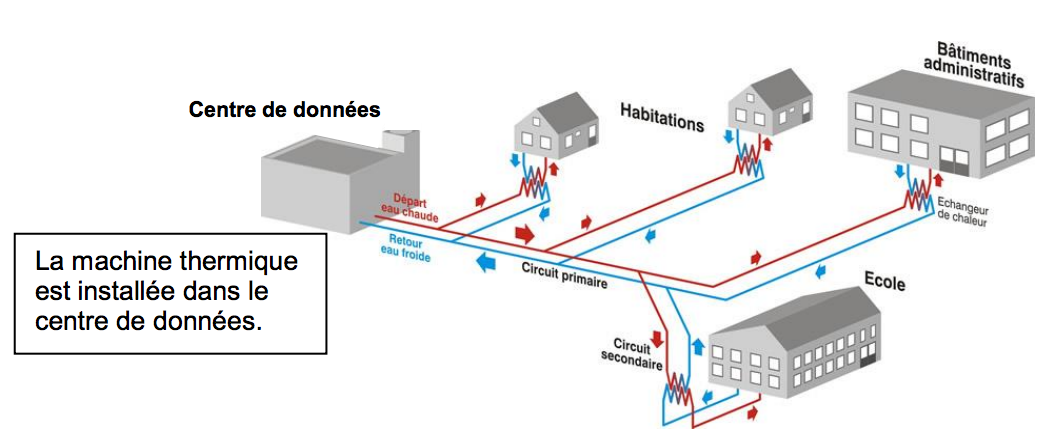
  Dans le cadre d’un modèle simplifié, les échanges énergétiques au niveau de la machine thermique peuvent être représentés sur le schéma ci-dessous :

  

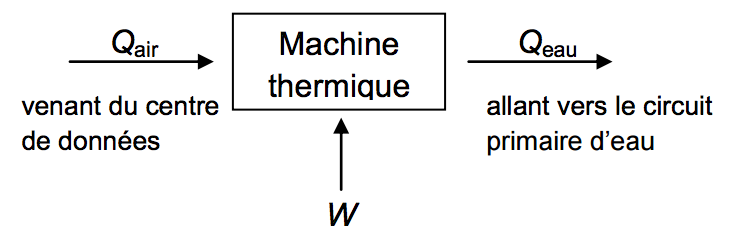
  avec :
  $Q_{air}$, énergie thermique fournie par l'air en une journée
  $Q_{air} = 5,2 \times 10^{11} \ J$
  $Q_{eau}$, énergie thermique reçue par l'eau en une journée
  $W$, énergie électrique reçue par la machine thermique en une journée
  $W = 1,0 \times 10^5 \ kWh$

  Sachant que la machine thermique ne fait que convertir sans perte l’énergie qu’elle reçoit, donner la relation entre $Q_{eau}$, $Q_{air}$ et $W$.

   

  3) Sachant que dans le circuit primaire l’eau entre dans la machine thermique à la température moyenne de $10°C$ pendant les $6$ mois de fonctionnement du chauffage des logements et bureaux, avec un débit de $2 \times 10^2 \ m^3.h^{-1}$, quel mode de chauffage peut-on envisager pour chauffer les logements voisins ?

  Toute démarche de résolution, même partielle, sera valorisée.

  Données :

  Mode de chauffage	Radiateur	Plancher chauffant
  Température de l'eau	$50°C$ à $65°C$	$25°C$ à $30°C$

   

  	Eau
  Capacité calorifique $(J.kg^{-1}.K^{-1})$	$4185$
  Masse volumique $(kg.m^{-3})$	$1,0 \times 10^3$

  Afficher la correction

  ---