PRIMITIVES, ÉQUATIONS DIFFÉRENTIELLES

Annales

• On désigne par $f$ la fonction définie sur l’intervalle $[−2 ; 4]$ par $f (x) = (2x +1) e^{−2x} +3$

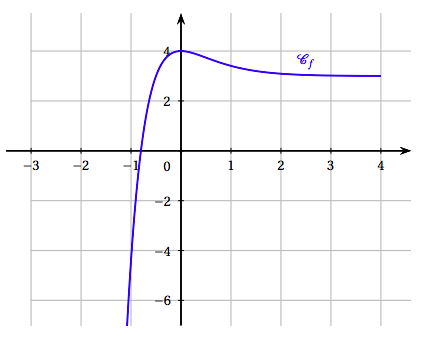
  On note $C_f$ la courbe représentative de $f$ dans une repère. Une représentation graphique est donnée en annexe.

   

  1. On note $f ′$ la fonction dérivée de $f$ . Montrer que, pour tout $x ∈ [−2 ; 4], f ′ (x) = −4xe^{−2x}$ 

  2. Étudier les variations de $f$.

  3. Montrer que l’équation $f (x) = 0$ admet une unique solution sur $[−2 ; 0]$ et donner une valeur approchée au dixième de cette solution.

  4. On note $f ′′$ la fonction dérivée de $f ′$. On admet que, pour tout $x ∈ [−2 ; 4], f ′′(x) = (8x −4)e^{−2x}$ 

     a. Étudier le signe de $f ′′$ sur l’intervalle $[−2 ; 4]$.

     b. En déduire le plus grand intervalle sur lequel $f $est convexe.

  5. On note $g$ la fonction définie sur l’intervalle $[−2 ;4]$ par $g (x) = (2x +1)e^{−2x}$ 

     a. Vérifier que la fonction $G$ définie pour tout $x ∈ [−2 ; 4]$ par $G(x) = (−x − 1)e^{−2x}$ est une primitive de la fonction $g$ .

     b. En déduire une primitive $F$ de $f$ .

  6. On note $A$ l’aire du domaine $D$ compris entre la courbe $C_f$, l’axe des abscisses et les droites d’équations $x = 0$ et $x = 1$.

     a. Hachurer le domaine $D$ sur le graphique donné en annexe.

     b. Par lecture graphique, donner un encadrement de $A$, en unité d’aire, par deux entiers consécutifs.

     c. Calculer la valeur exacte de $A$, puis une valeur approchée au centième.

   

  Annexe

  

  Afficher la correction

  ---