SUITES

Annales

• Annale bac 2021

   

  Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte.

   

  Question 1

  On considère les suites ($u_n$) et $(v_n)$ telles que, pour tout entier naturel $n$, 

  $u_n=1-\left(\dfrac{1}{4}\right)^n$    et   $v_n=1+\left(\dfrac{1}{4}\right)^n$

  On considère de plus une suite $(w_n)$ qui, pour tout entier naturel $n$, vérifie $u_n$≤$w_n$≤$v_n$. 

  On peut affirmer que :

  a. Les suites ($u_n$) et $(v_n)$ sont géométriques.

  b. La suite $(w_n)$ converge vers 1

  c. La suite ($u_n$) est minorée par 1

  d. La suite $(w_n)$ est croissante. 

   

  Question 2

  On considère la fonction $f$ définie sur $\mathbb{R}$ par : $f(x)=x{e^x}^2$

  La fonction dérivée de $f$ est la fonction $f$′ définie sur $\mathbb{R}$ par : 

  a. $f'(x)=2x{e^x}^2$                     b. $f'(x)=(1+2x){e^x}^2$

  c. $f'(x)=(1+2x^2){e^x}^2$          d. $f'(x)=(2+x^2){e^x}^2$

   

  Question 3

  Que vaut $\displaystyle \lim_{x \to +\infty}\dfrac{x^2-1}{2x^2-2x+1}$  ?

  a. $−1$               b. $0$                 c. $\dfrac{1}{2}$             d. $+\infty$

   

  Question 4

  On considère une fonction $h$ continue sur l’intervalle $[−1;1]$ telle que 

  $ℎ(−1)=0,\  ℎ(0)=2 $ et $ ℎ(1)=0$

  On peut affirmer que : 

  a. La fonction $ℎ$ est croissante sur l’intervalle $[−1 ;0]$

  b. La fonction $ℎ$ est positive sur l’intervalle $[−1 ;1]$

  c. Il existe au moins un nombre réel $a$ dans l’intervalle $[0;1]$ tel que $h(a)=1$

  d. L’équation $h(x)=1$ admet exactement deux solutions dans l’intervalle $[−1 ;1]$

   

  Question 5

  On suppose que $g$ est une fonction dérivable sur l’intervalle $[−4;4]$. 

  On donne ci-contre la représentation graphique de sa fonction dérivée $g'$. 

  

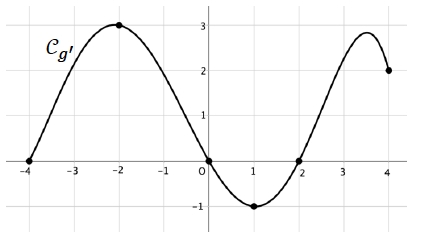
  On peut affirmer que : 

  a. $g$ admet un maximum en $−2$ 

  b. $g$ est croissante sur l’intervalle $[1;2]$

  c. $g$  est convexe sur l’intervalle $[1;2]$

  d. $g$ admet un minimum en $0$

  Afficher la correction

  ---