ANNALES DE SUJETS DE MATHÉMATIQUES

Annales

• Dans une boulangerie, les baguettes sortent du four à une température de 225 °C. 

  On s’intéresse à l’évolution de la température d’une baguette après sa sortie du four. 

  On admet qu’on peut modéliser cette évolution à l’aide d’une fonction $f$ définie et dérivable sur l’intervalle $[0 ;+∞[$ . Dans cette modélisation, $f(t)$ représente la température en degré Celsius de la baguette au bout de la durée $t$, exprimée en heure, après la sortie du four. 

  Ainsi, $f(0,5)$ représente la température d’une baguette une demi-heure après la sortie du four. 

  Dans tout l’exercice, la température ambiante de la boulangerie est maintenue à 25 °C. 

  On admet alors que la fonction $f$ est solution de l'équation différentielle $y'+6y=150$

   

  1. a. Préciser la valeur de $f(0)$. 

  b. Résoudre l’équation différentielle $y'+6y=150$

  c. En déduire que pour tout réel $t≥0$, on a $f(t)=200e^{-6t}+25$

   

  2. Par expérience, on observe que la température d’une baguette sortant du four :

  - décroît ; 

  - tend à se stabiliser à la température ambiante. 

  La fonction $f$ fournit-elle un modèle en accord avec ces observations ?

   

  3. Montrer que l’équation $f(t)=40$ admet une unique solution dans $[0 ; +∞[$ . 

  Pour mettre les baguettes en rayon, le boulanger attend que leur température soit inférieure ou égale à $40$ °C. On note $T_0$ le temps d’attente minimal entre la sortie du four d’une baguette et sa mise en rayon. 

  On donne ci-dessous la représentation graphique de la fonction $f$ dans un repère orthogonal.

  

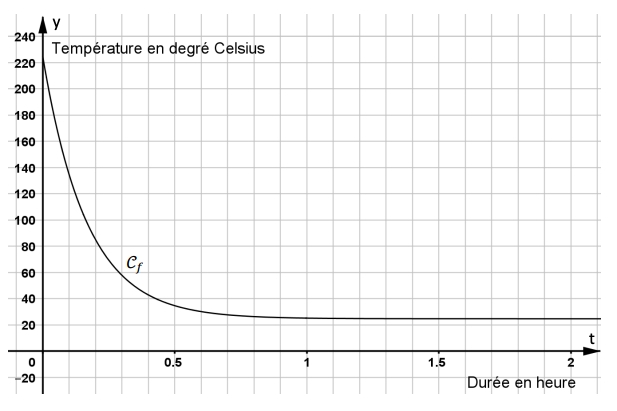
  4. Avec la précision permise par le graphique, lire $T_0$. On donnera une valeur approchée de $T_0$ sous forme d’un nombre entier de minutes. 

   

  5. On s’intéresse ici à la diminution, minute après minute, de la température d’une baguette à sa sortie du four. 

  Ainsi, pour un entier naturel $n$, $D_n$ désigne la diminution de température en degré Celsius d’une baguette entre la n-ième et la (n+1)-ième minute après sa sortie du four. 

  On admet que, pour tout entier naturel $n$

  $D_n=f\left(\dfrac{n}{60}\right)-f\left(\dfrac{n+1}{60}\right)$

  a. Vérifier que 19 est une valeur approchée de $D_0$ à 0,1 près, et interpréter ce résultat dans le contexte de l’exercice. 

  b. Vérifier que l’on a, pour tout entier naturel $n$ : $D_n= 200e^{-0,1n}(1-e^{-0,1})$

  En déduire le sens de variation de la suite $(D_n)$, puis la limite de la suite $(D_n)$. 

  Ce résultat était-il prévisible dans le contexte de l’exercice ? 

  Afficher la correction

  ---