ANNALES DE SUJETS DE MATHÉMATIQUES

Annales

• Exercice - Annale Bac 2017

  Partie A

  On considère la fonction $f$ définie sur l’intervalle $[0 ; 10]$ par $f (x) = \dfrac{1}{ 0,5+100e^{−x}}$ .

  On note $f′$ la fonction dérivée de $f$ sur l’intervalle $[0 ; 10]$.

  1. Montrer que, pour tout réel $x$ dans l’intervalle $[0 ; 10]$, on a $f'(x) =\dfrac{100e^{−x}}{ (0,5+100e^{−x})^2}$

  2 . On note $f ′′$ la fonction dérivée seconde de $f$ sur l’intervalle $[0 ; 10]$. Un logiciel de calcul formel fournit l’expression suivante de $f ′′(x)$ :$f ′′(x) =\dfrac{100e^{−x} (100e^{−x} −0,5)}{ (0,5+100e^{−x} )^3}$.

  2. a. Montrer que, dans l’intervalle $[0 ; 10]$, l’inéquation $100e^{−x} − 0,5 \geq 0$ est équivalente à l’inéquation $x\leq −\ln(0,005)$.

      b. En déduire le tableau de signes de la fonction $f ′′$ sur l’intervalle $[0 ; 10]$.

  3. On appelle $C_f$ la courbe représentative de $f$ tracée dans un repère. Montrer, à l’aide de la question 2, que la courbe $C_f$ admet un point d’inflexion noté $I$, dont on précisera la valeur exacte de l’abscisse.

  4. En utilisant les résultats de la question 2, déterminer l’intervalle sur lequel la fonction $f$ est concave.

   

  Partie B

  Dans toute cette partie les températures seront exprimées en degrés Celsius, notés °C.

  La COP21, conférence sur les changements climatiques des Nations Unies, a adopté le 12 décembre 2015 le premier accord universel sur le climat, appelé accord de Paris, signé par 195 pays. Cet accord confirme l’objectif, d’ici l’année 2100, que la température terrestre ne dépasse pas de plus de 2 °C la température de l’année 1900.

  Dans cette partie, on modélise, par la fonction $f$ de la partie A, une évolution de température possible permettant d’atteindre l’objectif de l’accord de Paris.

  La courbe représentative $C_f$ de la fonction est tracée ci-dessous, et $I$ est son point d’inflexion. Sur l’axe des abscisses, l’année 1900 correspond à 0 et une unité représente 25 ans, donc l’année 1925 correspond à 1. Sur l’axe des ordonnées, on a représenté le nombre de degrés Celsius au-dessus de la température de 1900. 

  

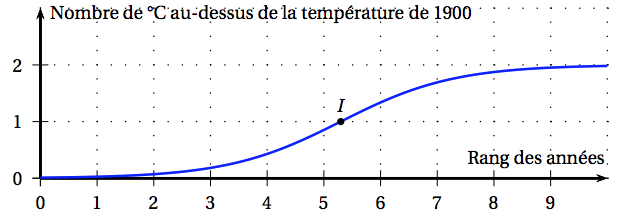
  1. a. Calculer $f (10)$, en arrondissant le résultat au centième.

      b. En déduire qu’en 2150, avec ce modèle, l’objectif de l’accord de Paris sera respecté.

  2. a. En utilisant la partie A, déterminer l’année correspondant à l’abscisse du point $I$ d’inflexion de la courbe $C_f$ . Arrondir le résultat à l’unité.

      b. Calculer, pour cette année-là, le nombre de degrés Celsius supplémentaires par rapport à 1900.

  3. On appelle vitesse du réchauffement climatique la vitesse d’augmentation du nombre de degrés Celsius. On admet que, à partir de 1900, la vitesse du réchauffement climatique est modélisée par la fonction $f ′ $.

      a. Est-il vrai de dire qu’après 2033 la température terrestre diminuera ? Justifier la réponse.

      b. Est-il vrai de dire qu’après 2033 la vitesse du réchauffement climatique diminuera ? Justifier la réponse.

  4. Pour sauvegarder les îles menacées par la montée des eaux, la température terrestre ne doit pas dépasser de plus de 1,5 °C la température de l’année 1900. Déterminer l’année au cours de laquelle la température terrestre atteindra ce seuil, selon ce modèle.

  Afficher la correction

  ---