ANNALES DE SUJETS DE MATHÉMATIQUES

Annales

• Annale bac 2021

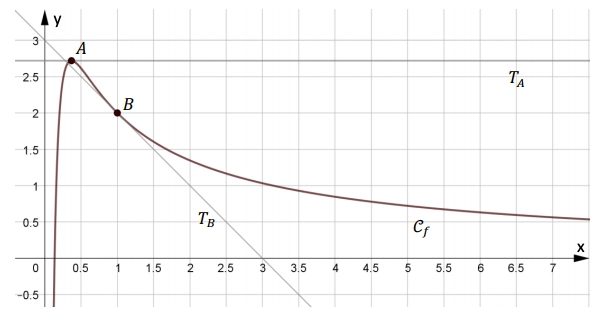
  Sur le graphique ci-dessous, on a représenté dans un repère orthonormé :

  – la courbe représentative $C_f$ d’une fonction $f$ définie et dérivable sur $]0 ; +∞[$ ;

  – la tangente $T_A$ à la courbe $C_f$ au point $A$ de coordonnées $(\dfrac{1}{e};e)$

  – la tangente $T_B$ à la courbe $C_f$ au point $B$ de coordonnées $(1 ; 2)$.

  La droite $T_A$ est parallèle à l’axe des abscisses. La droite $T_B$ coupe l’axe des abscisses au point de coordonnées $(3 ; 0)$ et l’axe des ordonnées au point de coordonnées $(0 ; 3)$.

  

  On note $f'$ la fonction dérivée de $f$.

  
  Partie I

  
  1. Déterminer graphiquement les valeurs de $f'(\dfrac{1}{e})$ et de $f'(1)$.
  
  2. En déduire une équation de la droite $T_B$

   

  Partie II

  
  On suppose maintenant que la fonction $f$ est définie sur $]0 ; +∞$[ par :

  $f(x)=\dfrac{2+\ln(x)}{x}$

  1. Par le calcul, montrer que la courbe $C_f$ passe par les points $A$ et $B$ et qu’elle coupe l’axe des
  abscisses en un point unique que l’on précisera.

  2. Déterminer la limite de $f(x)$ quand $x$ tend vers $0$ par valeurs supérieures, et la limite de
  $(f(x)$ quand $x$ tend vers $+\infty$.

  3. Montrer que, pour tout $x\in ]0 ; +∞[$ ,

  $f'(x)=\dfrac{-1-\ln(x)}{x^2}$

  4. Dresser le tableau de variations de $f$ sur $]0 ; +∞[$.

  5. On note $f$′′ la fonction dérivée seconde de $f$

  On admet que, pour tout $x\in ]0 ; +∞[$ ,

  $f''(x)=\dfrac{1+2\ln(x)}{x^3}$

  Déterminer le plus grand intervalle sur lequel $f$ est convexe.

  Afficher la correction

  ---