LE VECTEUR VITESSE (Accès libre)

Le vecteur vitesse - Partie 1

 

I. Caractéristiques du vecteur vitesse

 

La vitesse est une valeur. On lui ajoute maintenant une autre information : on dit que c'est un vecteur. En effet, le fait d’utiliser un vecteur pour décrire la vitesse permet d’avoir dans un seul objet plusieurs informations : un sens, une direction et une intensité/norme. Sur un schéma on représente un vecteur par une flèche.

 

 

Par exemple un wagon avance, il possède une vitesse qui va vers la droite : c’est dans cette direction que va le wagon. De même la Terre tournant autour du Soleil possède un vecteur vitesse à chaque instant.

En reprenant les caractéristiques d’un vecteur, on peut déduire les caractéristiques du vecteur vitesse $\overrightarrow{v}$ :

- la direction : elle doit être tangente à la trajectoire.

- le sens : sens du déplacement,

- la valeur/norme : vitesse en m/s,

Exemple : pour la direction, dans le cas du wagon on a bien la direction tangente à la trajectoire puisque celle-ci est rectiligne. Pour la Terre tournant autour du Soleil, il faut prendre la tangente à l’ellipse que parcourt la Terre au cours du temps.

Sur un schéma, on peut trouver la norme de la vitesse grâce à une échelle qui est donnée : par exemple si l’échelle indique que 1 cm correspond à 10 m/s alors si la longueur du vecteur sur le schéma est de 2 cm alors sa norme est de 20 m/s.

 

II. Lien avec le vecteur position

 

Rappel : formule importante à retenir : $v_{moy}= \dfrac{d}{\Delta t }$.

Où,

$v_{moy}$ est la vitesse moyenne en m/s,

$d$ est la distance parcourue en m,

$\Delta t$ est la durée du parcours en s,

C’est une vitesse moyenne car durant la durée du parcours, on ne connait pas la vitesse à chaque instant de l’objet.

 

Maintenant, si l’on connaît deux points successifs de l’objet :

 

 

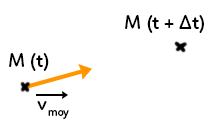
En reprenant la formule précédente on obtient : $v_{moy}=\dfrac{M(t)M(t+\Delta t)}{\Delta t}$.

En passant à la notion de vecteur, on peut faire l’analogie en remplaçant la vitesse moyenne par son vecteur correspondant et la distance par le vecteur correspondant : $\overrightarrow{v_{moy}}=\dfrac{\overrightarrow{M(t)M(t+\Delta t)}}{\Delta t}$.

 

Remarque : les deux vecteurs de cette équations sont proportionnels avec un coefficient de proportionnalité $ \frac{1}{\Delta t}$.

Ainsi $\overrightarrow{v_{moy}}$ et $\overrightarrow{M(t)M(t+\Delta t)}$ sont colinéaires.

On peut aussi écrire :

$\overrightarrow{v_{moy}}=\dfrac{\overrightarrow{OM}(t+\Delta t)- \overrightarrow{OM}(t)}{\Delta t}$

où $O$ est l’origine du repère. En effet, le point $M$ peut être représenté par son vecteur position ${\overrightarrow{OM}},$ et ce à chaque instant.

On peut montrer que c’est la même équation car :

$\overrightarrow{v_{moy}}=\dfrac{\overrightarrow{OM}(t+\Delta t)-\overrightarrow{OM}(t)}{\Delta t} $

$\overrightarrow{v_{moy}}=\dfrac{\overrightarrow{OM}(t+\Delta t)+\overrightarrow{MO}(t)}{\Delta t}$

$\overrightarrow{v_{moy}}=\dfrac{\overrightarrow{M(t)M}(t+\Delta t)}{\Delta t}$ grâce à la relation de Chasles.

 

Question optionnelle

On sait que $\overrightarrow{v_{moy}}$ et $\overrightarrow{M(t)M(t+\Delta t)}$ sont colinéaires.

Cela peut donner l’impression que la vitesse est liée à des succession de points $M,$ alors que dans la première partie il est dit que la vitesse est tangente à la trajectoire. Ainsi, on voit que soit la vitesse est soit définie grâce à une trajectoire, soit définie par une succession de points. Quel est le lien entre les deux ? (Réponse dans le cours suivant.)